z逆变换的定义
对于 z 变换的定义式为
$$
{X}({z}) \stackrel{\text { def }}= \sum_{n=-\infty}^{\infty}{x}({n}) z^{-n}
$$
则 z 逆变换由 $X ( z )$ 求其原序列 $x ( n )$ 的定义式为
$$
x ( n )=\frac{1} {2 \pi j} \oint_{c} \ X ( z ) z^{n-1} d z
$$
从定义上看,z 逆变换是一个围线积分,用积分求解不太现实,一般采用下面三种方法间接求 z 逆变换
幂级数展开法
幂级数展开法是根据 $Z$ 变换的定义式将 $F(z)$ 变换展开成下面形式的 $z^{ \pm 1}$ 幂级数:
$$
F(z)=\sum_{k=-\infty}^{\infty} f(k) z^{-k}=\cdots+f(-1) z^1+f(0) z^0+f(1) z^{-1}+\cdots
$$
那么序列 $f(k)$ 就是 $z^{ \pm k}$ 的系数。
$$
f(k)={\cdots, f(-2), f(-1), f(0), f(1), f(2), f(3), \cdots}
$$
$F(z)=\frac{1}{z}+\frac{1}{z^{5}}$
$$
F ( z )=\frac{1}{z}+\frac{1} {z^{5}} \leftrightarrow f ( k )={ 0, 1, 0, 0, 0, 1 }
$$
$F(z)=\frac{z^{4}-1}{z^{4}-z^{3}}$
对于这种有理多项式,可以采用长除法检验分子是否为分母的因式
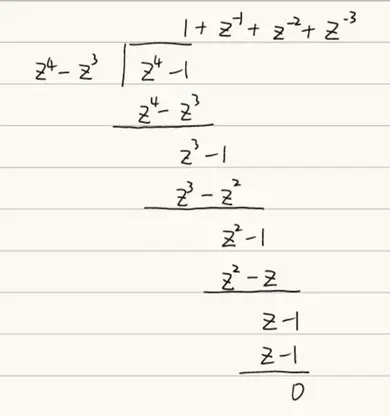
$$F(z)=1+z^{-1}+z^{-2}+z^{-3}$$
$$\therefore x(n)={1,1,1,1}$$
部分因式分解法
在离散信号分析中,一般像函数 $F(z)$ 可以写为 $z$ 的有理分式
$$
F(z)=\frac{e_m z^m+e_{m-1} z^{m-1}+\cdots+e_1 z+e_0}{z^n+d_{n-1} z^{n-1}+\cdots+d_1 z+d_0}=\frac{B(z)}{A(z)}
$$
根据代数学,只有真分式 $( n > m )$ 才能展开为部分分式,为此,当 $n=m$ 时 $\frac{F(z)}{z}$ 便是真分式。为了规范化,均展开 $\frac{F ( z )} {z}$ ,然后再乘以 $z$ 得 $F ( z )$ 的部分分式展开式
$$
\frac{F(z)}{z} = \frac{K_1}{z-a} + \frac{K_2}{z-b} + \frac{K_3}{(z-b)^2} + …
$$
然后通过常见信号的 z 逆变换以及 z 变换的性质去求逆变换。
例如,若 $\frac{F(z)}{z}=\frac{1}{z-a}$,则 $F(z)=\frac{z}{z-a} \leftrightarrow f(k)=a^k \varepsilon(k)$ (常用 z 逆变换)
而 $F(z)=\frac{1}{z-a} \leftrightarrow f(k)=a^{k-1} \varepsilon(k-1)$(z 变换的性质)
需要注意的是 $X(z)$ 的收敛域
$X(z)=\frac{z}{z^2-3z+2} ; |z| > 2$
$$
X(z)=\frac{z}{(z-1)(z-2)}=\frac{z}{z-2}-\frac{z}{z-1}
$$
由 $X(z)$ 的收敛域可知 $x(n)$ 为右边序列
$$
x (n)=\ 2^{n} u(n)-u(n)
$$
$X(z)=\frac{z}{z^2-3 z+2} ; |z|< 1$
$$
X ( {z} )=\frac{z}{( {z}-1 ) ( {z}-2 )}=\frac{z} {z-2}-\frac{z} {z-1}
$$
由 $X ( z )$ 的收敛域可知 $x ( n )$ 为左边序列,对于左边序列的变换公式和右边序列不同
$$
- a^{n} u (-n-1 ) \leftrightarrow\frac{z} {z-a} ; | z | < | a |
$$
$$
-u (-n-1 ) \leftrightarrow\frac{z} {z-1} ; | z | < | 1 |
$$
此时
$$
x ( n )=-2^{n} u (-n-1 ) \ +u (-n-1 ) = ( 1-2^{n} ) u (-n-1 )
$$
$X ( z )=\frac{z} {z^{2}-3 z+2} ; 1 < |z| < 2$
$$
X ({z} )=\frac{z}{(z-1 )(z-2 )}=\frac{z} {z-2}-\frac{z}{z-1}
$$
由 $X ( z )$ 的收敛域 $| z | < 2$ 可知极点 2 对应的是左边序列,$| z | > 1$ 可知极点 1 对应的是右边序列
$$
\therefore x ( n )=-2^{n} u (-n-1 )-u ( n )
$$
$X(z)=\frac{z}{(z-1)^2} ; |z|>1$
所用公式
$$
n u(n) \leftrightarrow \frac{z}{(z-1)^2}
$$
$X(z)=\frac{1-3 z}{(3 z-1)^2} ; |z|>\frac{1}{3}$
所用公式
$$
\quad n a^n u(n) \leftrightarrow \frac{z}{(z-a)^2}
$$
由z域尺度变换特性得
$$\left(\frac{1}{3}\right)^n n u(n) \leftrightarrow \frac{z / \frac{1}{3}}{\left(z / \frac{1}{3}-1\right)^2}=\frac{3 z}{(3 z-1)^2}$$
$$\therefore x(n)=n\left(\frac{1}{3}\right)^n u(n)$$
留数法
首先理解零极点的概念,对于刚刚提到的
$$F(z)=\frac{e_m z^m+e_{m-1} z^{m-1}+\cdots+e_1 z+e_0}{z^n+d_{n-1} z^{n-1}+\cdots+d_1 z+d_0}=\frac{B(z)}{A(z)}$$
- 令分子 $B(z)=0$ 的方程的解称为零点
- 令分母 $A(z)=0$ 的方程的解称为极点
- 由形如 $z^n、(z-a)^n$ 的得到的零极点称为 $n$ 重零(极)点
单极点与多重极点的求法
- $F(z) z^{k-1}$ 具有单极点 $\gamma_i(i=1,2, \cdots, n)$ 。
$$
{Res}\left[F(z) z^{k-1},\gamma_i\right]|{z=\gamma_i}=\left(z-\gamma_i\right) F(z) z^{k-1}|{z=\gamma_i}
$$
- $F(z)z^{k-1}$ 在 $z=\gamma_{i}$ 处具有 $r$ 重极点。重极点的留数为
$$
{Res}\left[F(z) z^{k-1} , \gamma_i \right]|{z=\gamma{i}}=\frac{1}{(r-1) !} \frac{\mathrm{d}^{r-1}}{\mathrm{~d} z^{r-1}}\left[\left(z-\gamma_{i}\right)^{r} F(z) z^{k-1}\right]|{z=\gamma{i}}
$$
右边序列的留数法
$$
{X}({z})=\frac{B(z)}{\left(z-p_1\right) \cdots\left(z-p_k\right)} ; |{z}|>\max \left[\left|p_k\right|\right]
$$
则: ${x}(n)=\left[\sum_k {Res}\left[X(z) z^{n-1}\right]_{z=p_k}\right]u(n)$
$X(z)=\frac{z}{(z-1)(z-2)},|z|>2$
先求 $X(z) z^{n-1}$ 的极点:
$$
X(z) z^{n-1}=\frac{z \times z^{n-1}}{(z-1)(z-2)}=\frac{z^n}{(z-1)(z-2)}
$$
令分母 $(z-1)(z-2)=0$,解得极点为: $z_1=1 ; z_2=2$
由收敛域 $|z|>2$ 可知序列 $n \ge 0$
此处 $n \ge 0$ 如何得来?
当 $n \le -1$ 时,我们可以知道实际上位于分子的 $z^n$ 这个时候是会跑到分母上变成 $n$ 阶极点。$n$ 阶极点的留数不好算,根据留数辅助定理,改算围线外极点留数,但是因为 $z_1 , z_2$ 此时均位于围线内,围线外无极点,故 $x(n)=0$
所以最后在合算的时候需要乘以 $u(n)$
$z_1=1$ 对应的留数为:
$$
\begin{array}{rlrl}
{Res}\left[X(z) z^{n-1}\right]{z=1} & =\left[\frac{(z-1) z^n}{(z-1)(z-2)}\right]{z=1} & k \text { 去极点 }
& =\left[\frac{1}{(z-2)} z^n\right]_{z=1}=-{1} & k \text { 代极点 }
\end{array}
$$
$z_2=2$ 对应的留数为:
$$
{Res}\left[X(z) z^{n-1}\right]{z=2}=\left[\frac{(z-2) z^n}{(z-1)(z-2)}\right]{z=2}=\left[\frac{1}{(z-1)} z^n\right]_{z=2}={2}^n
$$
由于两个极点都满足 $n \geq 0$
$$
\therefore x(n)=\left(2^n-1\right) u(n)
$$
$X(z)=\frac{2 z^2-3 z+1}{z^2-4 z-5};|z|>5$
$$X(z) z^{n-1}=\frac{2 z^2-3 z+1}{z^2-4 z-5} z^{n-1}$$
- 当 $n=0$ 时
$\left.X(z) z^{n-1}\right|_{n=0}=\frac{2 z^2-3 z+1}{z^2-4 z-5} z^{-1}=\frac{2 z^2-3 z+1}{z\left(z^2-4 z-5\right)}$
令 $X(z)$ 分母等于零, 得到三个极点:
$$
\begin{array}{ll}
z\left(z^2-4 z+5\right)=0 \rightarrow z(z-5)(z+1)=0 \
z_1=0 ;z_2=5;z_3=-1
\end{array}
$$
$z_1=0$ 对应的留数为:
$$
\operatorname{Res}\left[X(z) z^{-1}\right]{z=0}=\left[\frac{2 z^2-3 z+1}{(z-5)(z+1)}\right]{z=0}=-\frac{1}{5}
$$
$z_2=5$ 对应的留数为:
$$
\operatorname{Res}\left[X(z) z^{-1}\right]{z=5}=\left[\frac{2 z^2-3 z+1}{z(z+1)}\right]{z=5}=\frac{6}{5}
$$
$z_3=-1$ 对应的留数为:
$$
\operatorname{Res}\left[X(z) z^{-1}\right]{z=-1}=\left[\frac{2 z^2-3 z+1}{z(z-5)}\right]{z=-1}=1
$$
所以在 $n=0$ 时序列为 $x_1(n)=\left(-\frac{1}{5}+\frac{6}{5}+1\right) \delta(n)=2 \delta(n)$
- 当 $n \geq 1$ 时 $\left.\quad X(z) z^{n-1}\right|_{n \geq 1}=\frac{2 z^2-3 z+1}{z^2-4 z-5} z^{n-1}$
令 $X(z)$ 分母等于零, 得到2个极点:
$$
\left(z^2-4 z-5\right)=0 \rightarrow(z-5)(z+1)=0 \
z_1=5 ; z_2=-1
$$
$z_1=5$ 对应的留数为:
$$
{Res}\left[X(z) z^{n-1}\right]{z=5}=\left[\frac{2 z^2-3 z+1}{(z+1)} z^{n-1}\right]{z=5}=6(5)^{n-1}=\frac{6}{5}(5)^n
$$
$z_2=-1$ 对应的留数为:
$$
{Res}\left[X(z) z^{n-1}\right]{z=-1}=\left[\frac{2 z^2-3 z+1}{(z-5)} z^{n-1}\right]{z=-1}
$$
所以在 $n \geq 1$ 时序列为
$$
x_2(n)=\left[\frac{6}{5}(5)^n+(-1)^n\right] u(n-1)
$$
则所求序列为 $x(n)=x_1(n)+x_2(n)$
$$
\therefore x(n)=2 \delta(n)+\left[\frac{6}{5}(5)^n+(-1)^n\right] u(n-1)
$$
在 $n=0$ 时序列为 $x_1(n)=\left(-\frac{1}{5}+\frac{6}{5}+1\right) \delta(n)=2 \delta(n)$
将各极点在 $n=0, n \geq 1$ 时对应的样值合并,序列等效于
$$
x(n)=-\frac{1}{5} \delta(n)+\left[\frac{6}{5}(5)^n+(-1)^n\right] u(n)
$$
左边序列的留数法
$$
{X}({z})=\frac{B(z)}{\left(z-p_1\right) \cdots\left(z-p_k\right)} ; |{z}|<\min \left[\left|p_k\right|\right]
$$
则: ${x}(n)=\left[\sum_k -{Res}\left[X(z) z^{n-1}\right]_{z=p_k}\right]u(-n-1)$
还是这个题 $X(z)=\frac{z}{(z-1)(z-2)},|z|<1$
我改了一下收敛域,此时刚好与上题相反,当 $n \ge 0$ 时 $x(n) = 0$,当 $n \le -1$ 时与上面结果相反,差别是这个时候最后结果是乘以 $u(-n-1)$。
双边序列的留数法
$$
{X}({z})=\frac{B(z)}{\left(z-p_1\right) \cdots\left(z-p_k\right)} ; \min\left[|p_k|\right]|<|{z}|<\max \left[\left|p_k\right|\right]
$$
我们解析一下,实际上同样的分 $n \ge 0$ 和 $n \le -1$ 两种情况
当 $n \ge 0$ 时,我们知道此时的围线位于 $\min\left[|p_k|\right]|<|{z}|<\max \left[\left|p_k\right|\right]$ ,即围线内含有 $p_1 \to z$ 这些极点,我们求这些极点的留数,因为这是在 $n \ge 0$ 时成立
$$
{x}(n)=\left[\sum_{p_1}^{z} {Res}\left[X(z) z^{n-1}\right]_{z=p_k}\right]u(n)
$$
当 $n \le 0$ 时,此时围线内不仅包含 $p_1 \to z$ 这些极点,还包含 $n$ 阶极点 0 。根据留数辅助定理,我们改求围线外极点留数即
$$
{x}(n)=\left[\sum_{z}^{p2} -{Res}\left[X(z) z^{n-1}\right]_{z=p_k}\right]u(-n-1)
$$
最终合起来就是
$$
{x}({n})=\left[\sum_{p_1}^{z} {Res}\left[X(z) z^{n-1}\right]{z=p_k}\right]u(n)+\left[\sum{z}^{p2} -{Res}\left[X(z) z^{n-1}\right]_{z=p_k}\right]u(-n-1)
$$